Date: 28 Nov 2025
In classical machine learning, the goal of classification is simple, separate data points into different classes. Models try to find decision boundaries that divide one group from another. But as datasets grow large and complex, the relationships between features can twist, overlap, and hide within dimensions too small to fully express them. The key lies in lifting the data into higher dimensions, where hidden relationships become visible and separable.
Why Higher Dimensions Matter?
When data appears inseparable in its original form, it often means the space it lives in is too limited to reveal its true structure. By extending the data into a higher-dimensional space and subtle relationships that were once entangled can emerge with clarity. Patterns that overlap in low dimensions may become distinct when viewed from a broader perspective.
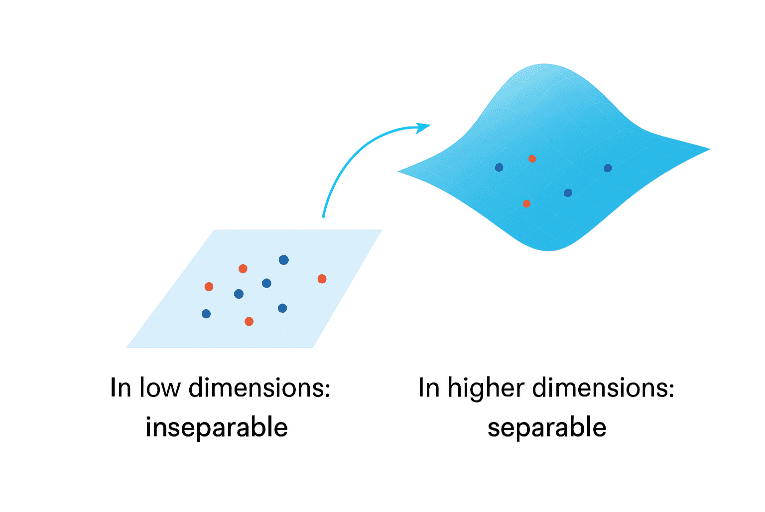
As shown, data that overlaps in a low-dimensional space can be separated in a higher-dimensional one, without relying on a specific dataset.
Higher dimensions don’t change the data itself, they change how the data is represented. This shift in perspective allows algorithms to discover new boundaries, define more expressive decision surfaces, and capture the deeper geometry of information.
In essence, higher dimensions offer a clearer lens through which complexity becomes order.
From Classical Feature Extraction to Quantum Feature Mapping
In classical machine learning, feature extraction highlights informative aspects of data, such as:
- In image processing: edges, textures, or colour histograms
- In-text analysis: embeddings like TF-IDF or Word2Vec to represent semantic meaning
These transformations expand the data’s representational space, helping models detect patterns that raw features might obscure. However, this expansion remains limited by classical computational frameworks. Quantum Feature Mapping takes this concept further.
Quantum systems embed classical data into Hilbert space, a mathematical construct so vast that even a few qubits represent exponentially many dimensions.
Within this expanded quantum space, data points that overlap in classical form can become linearly separable, enabling clearer boundaries and richer learning potential.
What Feature Mapping Really Means
Feature mapping is the process of transforming data from a lower-dimensional space into a higher-dimensional one, where hidden structures become easier to detect.
It doesn’t alter the underlying information. It changes how that information is expressed.
In higher dimensions, data gains the freedom to separate naturally, allowing algorithms to uncover relationships that were previously hidden.
Transitioning from Classical to Quantum Space
Quantum machine learning extends this concept into the quantum domain.
Each classical input is encoded as a quantum state:
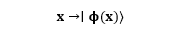
This mapping embeds classical data into the vastness of Hilbert space, where every quantum state corresponds to a unique high-dimensional vector. Subtle relationships between features — imperceptible to classical algorithms — can become separable within this quantum representation.
Balancing Power and Practicality
Every additional qubit doubles the dimensionality of the quantum state space.
This exponential growth grants extraordinary representational power, but also introduces practical constraints on today’s quantum hardware and classical simulators.
Efficient feature mapping is therefore essential: expressive enough to capture meaningful structure yet compact enough for real-world implementation.
Frameworks like Qiskit achieve this through parameterized quantum circuits, which encode classical data into quantum states in a controlled, tunable way.
These circuits make it possible to explore high-dimensional quantum behaviour while remaining computationally feasible.


