Date:18 Dec 2025
Here is the second excerpt from the book Quantum Communications by Gianfranco Cariolaro.
In this blog, we trace the journey that transformed physics from the classical crisis at the dawn of the 20th century to the revolutionary discoveries that shaped modern Quantum Mechanics. This narrative highlights the foundational breakthroughs that not only resolved long-standing mysteries but also opened the door to the quantum era.

Classical Crisis and Planck’s Revolution
In the late 19th century, physicists were confident that classical theories including Newton’s mechanics and Maxwell’s electromagnetism are sufficient to explain everything. However, these theories didn’t explain minor issues, most notably the way hot objects (black bodies) emit light.
Based on classical theory, the Rayleigh-Jeans Law specifically calculated low-frequency radiation to be either visible or infrared. When applied to high frequencies (ultraviolet and beyond), the theory predicted a result: infinite energy being emitted, a failure famously dubbed the ultraviolet catastrophe.
To solve this physical impossibility, Max Planck in 1900 introduced a radical, purely mathematical fix: he hypothesized that radiating energy is not continuous, but exists only in discrete, tiny packets, he called quanta. The energy associated with each quantum is linearly dependent on the radiation frequency
, with Planck’s constant
defining the proportionality:
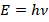
This hypothesis led to Planck’s Law, which perfectly matched experimental data at all frequencies.
Quanta Validation
Planck’s idea was initially seen as just a mathematical trick, but the later discoveries validated his findings.
Albert Einstein used the concept of quanta (later called photons) to fully explain the photoelectric effect, establishing a discrete, particle-like nature of light as a fundamental concept.
Niels Bohr applied the idea to the structure of the atom in 1913. He hypothesized that an electron’s transition between discrete energy levels explains why atoms only emit light at specific, characteristic frequencies, correctly interpreting the hydrogen spectrum.
The Wave-Particle Leap
The final step in this pioneering phase came from Louis de Broglie in 1924, who extended this wave-particle duality, suggesting that not only does light sometimes act as a particle, but particles like electrons can also behave as waves. This dual nature became formalized by the de Broglie relation:
(λ=h/mv)
This relation links the wavelength (λ) of a particle to its momentum (mv), concluding the early phase of Quantum Theory.
The Maturity Phase: Formalizing the Mathematics
In the 1920s and 1930s, the theory matured into the formal discipline of Quantum Mechanics:
Erwin Schrödinger developed the wave equation, which is the mathematical basis for describing the state and evolution of systems in Qunatum Mechanics.
Werner Heisenberg introduced the Uncertainty Principle, stating that observing a particle inherently changes its state, making it impossible to simultaneously know both its position and momentum with perfect accuracy. This statistical and uncertain view of nature became a fundamental reality.
The entire framework required a new mathematical context, which was provided by the mathematician David Hilbert, establishing the need for Hilbert spaces.


